Zauberwürfel-Grundlagen: Konjugation und Kommutatoren

Dieser Artikel erschien 2015 in meinem alten Rolandroid-Blog. Hier die aktualisierte und ergänzte Fassung:

Die letzten paar Wochen habe ich mich etwas mit den Grundlagen des Zauberwürfels zu beschäftigen versucht, also etwas Cube-Theorie. Aber keine Sorge, dieser Artikel und die Videos wollen vermeiden, allzu theoretisch zu werden. Mich hat vielmehr interessiert, inwieweit ein paar logische Überlegungen helfen können, den Zauberwürfel auch ohne auswendig gelernte Zugfolgen lösen zu können, sondern quasi intuitiv. So weit bin ich zwar noch lange nicht, aber immerhin habe ich jetzt einigermaßen verstanden, was mit Kommutatoren gemeint ist und was mit Konjugation. In den Videos zeige ich dazu praktische Anwendungsmöglichkeiten. Da ich dabei aber noch ganz am Anfang stehe, freue ich mich natürlich auch über erweiternde Kommentare unter diesem Artikel.

Kommutatoren

Unter Kommutatoren versteht man die Anwendung zweier Algoritmen A und B, die hintereinander ausgeführt werden, und danach wieder rückwärts (A‘ und B‘) ausgeführt werden, also A, B, A‘, B‘.

Ein Video von RedKB hat mich darauf gebracht, aber die praktische Anwendung wurde mir erst in einem Video von Tony Fisher (ab Minute 7:30) klar. Deshalb versuche ich hier eine einigermaßen verständliche und einigermaßen deutschsprachige 😉 Erklärung:

Das Thema Konjugation wird im Video ja auch schon gezeigt. Trotzdem hier auch noch ein paar schriftliche Erläuterungen, bevor dann das zweite Video eine praktische Anwendung zeigt:

Konjugation (Setup Moves)

Die Konjugation ist mit den Kommutatoren irgendwie verwandt. Mathematiker mögen gerne in den Kommentaren unter diesem Artikel den Zusammenhang genauer erklären. 🙂 Mir geht es nur darum, dass sie dem Aufbau A, B, A‘ folgen – wobei Zugfolge A ein sogenannter Setup Move oder Vorbereitungszug ist. Mit dem Setup Move werden die Steine so positioniert, dass sich dann ein bereits bekannter Algoritmus B sinnvoll anwenden lässt. Danach muss man dann den Setup Move wieder zurücknehmen (A‘). Einentlich ganz simpel, und man kann schöne Sachen damit machen – beispielsweise das berühmte Würfel-im-Würfel-Muster:

Das Muster gab es übrigens schon zweimal hier im Blog: Einmal – wie im Video erwähnt, als Muster 18 meiner Zauberwürfel-Muserkollektoin. Und schon einmal hier: Würfel im Würfel.

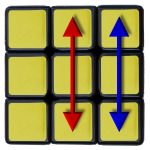
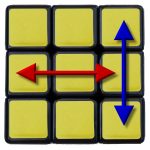Eine ebenfalls sehr schöne Anwendung von Setup-Moves ist mein neuer F-Perm (siehe links). Er besteht aus einem Setup-Move, dann dem T-Perm (siehe rechts) und dann der Rücknahme des Setups:

R‘ U‘ F‘ (R U R‘ U‘  R‘ F R2  U‘ R‘ U‘  R U R‘ F‘) F U R

Mit dem Setup-Move R‘ U‘ F‘ werden also die 2 Ecken und 2 Kanten, die jeweils getauscht werden sollen, aus der F-Perm-Position so umgestellt, dass sie dann mit dem (eingeklammert geschriebenen) T-Perm getauscht werden können.
Danach wird mit F U R der Setup-Move wieder rückwärts durchgeführt. Die beiden grau geschriebenen Drehungen F‘ und F kann man in der Praxis natürlich weglassen, da sie sich ja gegenseitig aufheben.

So, ich hoffe, dieser Ausflug in die Grundlagen hat Euch gefallen. Für Fragen, Anregungen, Meckerei oder Lobeshymnen gibt es wie immer die Kommentarfunktion.