4x4x4 und 5x5x5, Speedcubing für Anfänger (Hoya-Methode)

NEU (Januar 2022): In meinem neuen Cubing-Blog  freshcuber.wordpress.com gibt es eine aktualisierte Version dieses Artikels. Einfach hier klicken:

4x4x4, Speedcubing für Anfänger (Hoya-Methode)

und

5x5x5, Speedcubing für Anfänger (Hoya-Methode)

◊ ◊ ◊

Hier folgt nun die alte Version des Artikels mit den Links in den alten Blog:

Dieser Artikel wurde überarbeitet. Der 4×4 und der 5×5 haben jetzt jeweils einen eigenen Artikel. Dadurch wird es übersichtlicher und es konnte stellenweise noch etwas verständlicher erklärt werden:

• 4x4x4, Speedcubing für Anfänger (Hoya-Methode)
• 5x5x5, Speedcubing für Anfänger (Hoya-Methode)

Hier folgt nun die alte Version des Artikels:

Tutorial in 5 Schritten: [4 Centerfelder] [4 weiße Kantenpaare]
[2 Centerfelder] [8 Kantenpaare] [3×3-Teil und Parity]

In diesem Artikel möchte ich zeigen, wie man den 4×4-Zauberwürfel – früher Rubik’s Master Cube oder Rubik’s Revenge genannt – löst. Und weil es auf dem 5×5 – Professor’s Cube – fast das Gleiche ist, zeig ich es für den gleich mit.

Zwar hatte ich früher im alten Blog schon ein Anfänger-Lösungssystem als Video (4×4 und 5×5) und als 4×4-Spickzettel vorgestellt, doch inzwischen habe ich 5 Jahre mehr Erfahrung, und ich bin überzeugt, dass man auch als 4×4- oder 5×5-Anfänger gut mit der Hoya-Methode der Speedcuber zurechtkommt. Es ist nicht wirklich komplizierter, aber deutlich schneller. Dadurch, dass man erst die weißen Kanten alle auf die Unterseite bringt und sich danach erst auf die restlichen Kanten konzentriert, ist es auch strukturierter und damit gerade für Anfänger übersichtlicher.

Das Grundprinzip der Hoya-Methode ist außerdem gleich wie bei reinen Anfängermethoden: Reduktion des 4×4 oder 5×5 auf einen 3×3. Wenn man alle Center und alle Kanten farblich sortiert hat, dreht man nur noch die Außen-Layer und kann ihn im Prinzip wie einen 3×3 lösen, von einzelnen Parity-Problemen mal abgesehen (die es aber bei Anfängerlösungen genauso gibt). Um das Lösen des 4×4 oder 5×5 zu lernen, sollte man daher bereits in der Lage sein, den 3×3 sicher lösen zu können; egal ob mit Anfängermethode oder Fridrich, etc.

Ich werde nun zu den einzelnen Schritten jeweils einige Erklärungen abgeben. Aber die Details entnehmt Ihr bitte dem Video zum jeweiligen Abschnitt.

Grundsätzliches

Der 4×4-Zauberwürfel hat – wie alle geradzahligen Cubes, also auch 6×6, 8×8, etc. – keinen festen Mittelstein auf jeder Seite. Daher kann man die Center der ersten Farbe hinlegen, wo man möchte. Ab dem zweiten Centerfeld muss man dann aber darauf achten, dass es richtig in Bezug auf das Erste steht.

Da auf den äußeren Layern die Ecken und Kanten sitzen, müssen pro Farbe 4 Center zusammengebracht werden. Wir haben also 6 Centerfelder a 4 Steinen, somit 24 Centersteine. Zunächst werden wir aber nur 4 der 6 Centerfelder lösen.

Beim 5×5 sind zwar mehr Center und mehr Kanten zu sortieren (9 Centersteine auf jeder der 6 Seiten und 3 Kantensteine auf jeder der 12 Kanten). Aber dadurch, dass es feste Mittelsteine gibt, entfällt das Problem mit der Anordnung der Farben. In dieser Hinsicht ist er sogar einfacher als der 4×4.

Auch wenn es beim 5×5 jeweils 3 Kantensteine mit den gleichen Farben gibt, nenne ich diese 3er-Gruppe der Einfachheit halber auch Kantenpärchen. Oder wäre Euch „Kantendreiergrüppchen“ lieber? 😉

Bei der Hoya-Methode, wie ich sie anwende und auch Anfängern erkläre, gehen wir beim Lösen der Center nicht völlig farbneutral vor, sondern lösen den 4×4 (und den 5×5) in folgenden 5 groben Schritten:

Schritt 1: Vier Centerfelder lösen
(alle außer Gelb und ein angrenzendes Centerfeld)

• Erstes Centerfeld lösen mit einer der seitlichen Farben auf dem Cube, also Rot, Grün, Orange oder Blau. Am besten mit einem beginnen, das schon teilweise fertig ist, weil es z.B. schon ein farblich passendes Centerpärchen gibt.
• Das fertige erste Centerfeld jetzt nach unten halten und gegenüber liegend, also oben, das zweite Centerfeld lösen, mit der Gegenfarbe, die auch auf dem normalen 3×3-Würfel gegenüber ist. Wenn man z.B. mit Rot begonnen hat, dann kommt gegenüber Orange hin.
• Nun werden die beiden gelösten Centerfelder rechts und links gehalten und als dritte Seite das dritte Centerfeld, weiß, gelöst.
• Dann kommt das vierte Centerfeld, das auf einer Seite an die weiße Seite angrenzt. Wenn rechts und links z.B. Rot und Orange sind, dann entweder Blau oder Grün. An dieser Stelle muss man sehr aufpassen, dass man die richtige Farbe entsprechend dem Farbschema des Würfels wählt.

Schritt 2: Vier weiße Kantenpaare lösen (weißes Kreuz)

• Nun drehen wir weiß nach unten und die beiden noch ungelösten Centerfelder halten wir so, dass sie vorne und oben sind. Jetzt werden auf der Unterseite nacheinander und in der richtigen Reihenfolge die Kantenpärchen mit weiß gebildet, also rot-weiß, grün-weiß, orange-weiß und blau-weiß.

Schritt 3: Die restlichen 2 Centerfelder lösen (Gelb und was übrig bleibt)

• Das weiße Kreuz nun an den seitlichen Centern ausrichten. Um jetzt Platz zu schaffen für die beiden noch verbliebenen Centerfelder, machen wir folgenden Vorbereitungszug: F L.
• Nun können die beiden verbliebenen Centerfelder sortiert werden. Wenn man oben gelb zusammenbaut, sollte vorne die verbliebene sechte Farbe automatisch übrig bleiben.
• Mit L‘ F‘, also der Rücknahme des Vorbereitungszuges, werden die beiden in Sicherheit geparkten weißen Kantenpaare wieder an ihren Platz gebracht. Nun sind alle Center und die weißen Kanten korrekt.

Schritt 4: Die acht restlichen Kantenpaare lösen

• Nun werden die restlichen 8 Kantenpaare gebildet – je nach persönlichem Fortschritt einzeln, paarweise, oder mit der 3-2-3-Methode auf dem 4×4 und mit „FreeSlice“ auf dem 5×5.
• Auf dem 5×5 bleibt eventuell ein einzelnes ungelöstes Kanten-Dreierpärchen übrig, das man mit einem OLL-Parity-Zug lösen kann.

Schritt 5: Wie ein 3×3 lösen, und wenn nötig
OLL-Parity und/oder PLL-Parity beseitigen

• Jetzt sind alle Centerfelder und Kantenpaare korrekt, und der Cube kann wie ein 3x3x3 gelöst werden, indem man nur noch die äußeren Layer dreht.
• Beim gelben Kreuz auf dem 4×4 bleibt in 50% der Fälle eine ungerade Zahl gelber Kantenpaare übrig. Dann hat man „OLL-Parity“ und kann mit einem bestimmten Zug ein einzelnes Kantenpaar wenden.
• Ebenfalls in 50% der Fälle tritt am 4×4 „PLL-Parity“ auf, wenn z.B. am Ende nur 2 Ecken oder 2 Kantenpaare getauscht werden müssen. Auch dafür gibt es einen (recht einfachen) Algorithmus. Spätestens jetzt sollte der 4×4 gelöst sein.

Es klingt alles komplizierter als es ist. Ich werde die einzelnen Schritte noch ausführlich erklären und bebildern, sowie mit fresh gecubten Erklärbär-Videos garnieren. 😉

Schritt 1: Vier Centerfelder lösen

Zunächst werden die Center von 4 der 6 Seiten gelöst. Nur Gelb und eine angrenzende Seite lassen wir übrig für später.

1.1) Erstes Centerfeld lösen

Erst einmal nutzen wir die Inspektionszeit und überlegen, mit welcher seitlichen Farbe wir beginnen möchten. Also Rot, Grün, Orange oder Blau.
Und nicht Gelb oder Weiß, denn das sind ja die Farben der Ober- bzw. Unterseite.

Es bietet sich an, danach zu schauen, ob man schon irgendwo ein 2er-Pärchen von gleichfarbigen Centern entdeckt. Dann dieses auf die Oberseite stellen und schauen, wie man die anderen beiden Center dieser Farbe nebeneinander bekommt und dann als Paar neben das erste Paar stellen kann.

Hier im Beispiel beginnen wir mit Rot. Später solltet Ihr aber mit einer beliebigen der 4 genannten seitlichen Farben des Würfels beginnen, und zwar mit der, die möglichst günstig steht.

1.2) Zweites Centerfeld lösen

Wenn das erste Centerfeld fertig ist, drehen wir den Würfel so, dass es unten ist, und machen auf der Oberseite das Centerfeld mit der Gegenfarbe, die auch auf dem normalen 3×3-Würfel gegenüber ist. Wenn man z.B. mit Rot begonnen hat, dann kommt gegenüber Orange hin.

Dies ist jetzt nicht mehr ganz so einfach, denn wir müssen ja aufpassen, dass wir das Centerfeld auf der Unterseite nicht wieder zerstören. Aber mit dem üblichen „öffnen, reindrehen, schließen“ wie in der 3×3-Anfängermethode lässt sich auch hier einiges erreichen.

Wichtig: Immer dran denken, wenn Ihr „öffnet“ (mit Rw‘ oder Lw), gehen unten (und ggf. hinten) die bereits gelösten Centerfelder kurzfristig auseinander, bis Ihr wieder „schließt“ (mit Rw bzw. Lw‘). Also das Schließen besser nicht vergessen…

Im Video am Ende des Abschnitts wird dies deutlicher.

1.3) Drittes Centerfeld lösen (weiß)

Nun werden die beiden gelösten Centerfelder rechts und links gehalten und als dritte Seite das dritte Centerfeld, weiß, gelöst. Dadurch, dass wir die beiden fertigen Centerfelder rechts und links halten, gehen sie nicht kaputt, wenn wir den Würfel nun „wie ein Spanferkel“ 😉 um die waagerechte Achse rotieren und auch nur in dieser Richtung Wide-Turns machen (Rw, Lw, etc.).

1.4) Viertes Centerfeld lösen

Dann kommt das vierte Centerfeld, das auf einer Seite an die weiße Seite angrenzt. Wenn rechts und links z.B. Rot und Orange sind, dann entweder Blau oder Grün. An dieser Stelle muss man beim 4×4 sehr aufpassen, dass man die richtige Farbe entsprechend dem Farbschema des Würfels wählt. Wer nicht glaubt, dass Blau hier im Bild die richtige Farbe ist, der halte einen normalen (gelösten) Zauberwürfel so, dass Weiß oben und Rot links ist. Dann ist Blau vorne (und nicht Grün).

Vier Center sind jetzt gelöst – die drei auf dem Bild sichtbaren und das orange Centerfeld gegenüber von Rot, also rechts auf dem Würfel. Die beiden fehlenden (hinten und unten) kommen später dran.

Hier nun das Video, das diesen Ablauf im Detail zeigt – sowohl für den 4×4 (in den ersten 16 Minuten) als auch für den 5×5 (von Minute 16 bis 29):

Schritt 2: Vier weiße Kantenpaare lösen

Ab hier halten wir Weiß nach unten und die beiden noch nicht gelösten Centerfelder so, dass sie oben und vorne sind. Wir stellen eine der beiden rot-weißen Kanten unter das ungelöste Centerfeld der Vorderseite, und zwar so, dass ihre weiße Seite auf der Unterseite ist (und Rot somit vorne). Nun suchen wir die zweite rot-weiße Kante und stellen sie oben an die vordere Kante, also zwischen die ungelösten Center.

Keine Angst: Solange wir (außer bei Rw, Lw…) nur die äußeren Ebenen des Würfels drehen, um die Kanten zu positionieren, bleiben die Center unverändert.

Wenn der obere rot-weiße Kantenstein weiß nach vorne zeigt, ist das die günstigere Position, denn dann stehen die beiden Kanten schon farblich richtig zueinander, also in verschiedenen Ebenen.

Im links abgebildeten Fall machen wir U Rw U‘ Rw‘, also Kante links zwischenparken, dann rechts den Slot öffnen, Kante eindrehen und Slot wieder schließen.

Im Rechts abgebildeten Fall genau spiegelbildlich, also U‘ Lw‘ U Lw. Kante rechts zwischenparken, dann links den Slot öffnen usw.

In beiden Fällen wird die Kante beim ersten Zug möglichst zur weiter entfernt liegenden Seite gebracht, also gegenüber von dem Slot, der geöffnet wird. Das hat den Vorteil, dass man 2 Ebenen gleichzeitig drehen kann. Würde man die Kante auf der anderen Seite zwischenparken, dann darf man beim Öffnen des Slots nur die innere Ebene drehen, weil sich sonst die zwischengeparkte Kante mit nach hinten dreht. Also:

Im links abgebildeten Fall U‘ r U r‘
Im rechts abgebildeten Fall U l‘ U‘ l

Nun bleiben noch die beiden Fälle, wo das Weiß des oberen Kantensteins nach oben zeigt. Das ist im Prinzip wie bei der weißen Ecke in der 3×3-Anfängerlösung: Wir brauchen einen Zwischenschritt, um sie zu wenden.

Im links abgebildeten Fall machen wir Rw U2 Rw‘, und dann weiter wie oben beschrieben, also mit U Rw U‘ R.

Im rechts abgebildeten Fall machen wir Lw‘ U2 Lw, und dann weiter wie oben beschrieben, also mit U‘ Lw‘ U Lw.

Um sich den Zwischenschritt möglichst sparen zu können, achtet man mit der Zeit immer mehr darauf, beim Positionieren der oberen Kante diese möglichst gleich so zu stellen, dass ihre weiße Fläche nach vorne zeigt.

Wenn das erste Kantenpaar (rot-weiß) erstellt wurde, wird es mit D‘ auf die linke Seite gestellt und vorne ist nun Platz für das zweite Kantenpaar. Rechts von rot-weiß kommt nun grün-weiß.

Natürlich muss man beim Positionieren der grün-weißen Kanten darauf achten, das rot-weiße Kantenpaar links unten am Platz zu lassen.

Wenn grün-weiß fertig ist, wieder ein D‘, um Platz für orange-weiß zu machen. Und danach wieder für blau-weiß.

Nun müsste unten ein komplettes weißes Kreuz in der richtigen Anordnung stehen. Und nach wie vor sollten 4 der 6 Centerfelder geordnet sein, wenn Ihr immer schön brav die Kantenpaare nur unter den ungeordneten Centerfeldern gebildet habt.

Am besten das weiße Kreuz an den Centern ausrichten und mal einen kleinen Kontrollblick auf die Unterseite wagen. Das ist doch eine gute Basis für den letzten Hauptschritt, den 3×3-Lösungsteil.

Und hier das Video zu Schritt 2. Bis Minute 10 am 4×4, von Minute 10 bis 15 am 5×5:

Schritt 3: Die restlichen 2 Centerfelder lösen

Das weiße Kreuz (wie gesagt) an den seitlichen Centern ausrichten. Um jetzt Platz zu schaffen für das Sortieren der beiden noch verbliebenen Centerfelder, machen wir folgenden Vorbereitungszug: F L. Dadurch werden die gelösten weißen Kanten in Sicherheit gebracht und man kann oben und vorne werkeln (U und F, und Rw/Rw‘ sowieso), ohne sich die weißen Kantenpaare wieder zu zerlegen.

Nun sortieren wir also die 4 gelben Centersteine nach oben. Im Prinzip läuft das genauso wie bei den früheren Centern. Wenn man oben gelb zusammenbaut, sollte vorne die verbliebene sechste Farbe automatisch übrig bleiben

Mit L‘ F‘, also der Rücknahme des Vorbereitungszuges, werden die beiden in Sicherheit geparkten weißen Kantenpaare wieder an ihren Platz gebracht. Nun sind alle Center und die weißen Kanten korrekt.

Und hier das Video zu Schritt 3:

Schritt 4: Die acht restlichen Kantenpaare lösen

Das Lösen der verbliebenen 8 Kantenpaare verläuft beim 4×4 etwas anders als beim 5×5, obwohl sich die Techniken ähneln. Schauen wir zunächst auf den 4×4:

Je nach persönlicher Erfahrung kann man die Kantenpaare einzeln, paarweise oder gar 3 zusammen lösen. Ich bemühe mich im Video zu Schritt 4, alle Varianten zu zeigen. Allerdings muss ich zugeben, dass ich mit diesem Video noch nicht wirklich zufrieden bin; das hätte doch etwas strukturierter sein können. Daher zunächst ein paar Anmerkungen und Tipps zum „Edge Pairing“:

Das wichtigste „Handwerkszeug“ sind folgende 3 Algorithmen:

• Kante von oben nach rechts „vorwärts“ einbauen (also dass sie so steht, wie sie bei einer einfachen F-Drehung stehen würde, allerdings ohne Center und weißes Kreuz zu zerstören): F R‘ F‘ R
• Kante von oben nach rechts „rückwärts“ einbauen (also so, dass sie genau andersherum steht): R U‘ R‘
• Kanten-Flip rechts, also Wenden der Kante: R U R‘    F R‘ F‘ R

Von dem „Rückwärts“-Zug verwende ich auch gerne mal die gespiegelte Version L‘ U L oder wende ihn für die hinteren Slots so an: R‘ U R bzw. L U‘ L‘. Es ist nichts Anderes als „öffnen, reindrehen, schließen“ in den verschiedensten Variationen.

Wie man sieht, ist der Kantenflip nichts Anderes als eine Kombination der ersten beiden Züge: Zunächst wird der 2. Algo rückwärts angewendet, um die rechte Kante vorne auf die Oberseite zu bringen. Und dann wird sie mit dem 1. Algo vorwärts wieder versenkt.

Los geht’s. Folgende Möglichkeiten gibt es (und werden im Video gezeigt):

4×4: Kanten-Paare einzeln bilden

Die beiden zusammengehörenden Kantensteine werden rechts und links auf der Frontseite positioniert, und zwar so, dass sie diagonal stehen. Also einer auf der 2. Ebene von oben, der andere auf der 2. Ebene von unten.

Nun kann man sie mit Uw bzw. Uw‘ übereinander drehen (Center gehen dabei auseinander). Jetzt das nun gelöste Pärchen mit „öffnen, reindrehen, schließen“ durch eine ungelöste Kante ersetzen. Danach nimmt man den Uw- bzw. Uw‘-Zug wieder zurück, damit die Center wieder okay sind.

Alternativ kann man auch erst die Center mit Uw bzw. Uw‘ öffnen und dann die Kante mit dem farblich passenden Stück von der Oberseite so einbauen, dass das neue Pärchen beim Schließen der Center entsteht.

Wenn alle 4 „Parkplätze“ für gelöste Kantenpärchen auf der Oberseite besetzt sind, baut man 2 davon in die beiden hinteren Slots ein, so dass nochmal 2 ungelöste Kanten oben stehen.

4×4: Letzte 2 Kantenpaare lösen

Wenn nur noch 2 Kantenpaare ungelöst sind, müssen diese gleichzeitig gelöst werden, denn es gibt ja keine „freien Parkplätze“ mehr auf der Oberseite, also keine ungelösten Kanten zum Ersetzen eines Pärchens.

Daher werden die beiden Kanten nun so in die beiden vorderen Slots gestellt, dass die gleichfarbigen Steine nicht diagonal sondern gerade gegenüber auf der Vorderseite stehen. Dann macht man Uw‘ und den obigen Kanten-Flip und danach Uw. Komplett also:

Uw‘ (R U R‘ F   R‘ F‘ R) Uw

4×4: Jeweils 2 Kanten-Paare lösen

Effektiver als jedes Pärchen einzeln zu bilden ist es natürlich zu lernen, die Kanten paarweise zu lösen. Wer ausreichend gut Englisch kann, lässt es sich am Besten vom Weltmeister erklären: Cubeskills, 2 Edge Pairing, denn meine Erklärungen hierzu sind in meinem folgenden Video doch seeehr dürftig. Wenn Ihr seht, wie oft die von Feliks Zemdegs vorgestellte Anfängermethode den Würfel auf den Kopf stellt, dann versteht Ihr vielleicht, wieso ich meine, auch als Anfänger sollte man lieber die Hoya-Methode lernen (oder die von Feliks bevorzugte Yau-Methode, die recht ähnlich ist, aber für Anfänger vielleicht doch nicht ganz so gut geeignet).

Um 2 Kanten quasi gleichzeitig zu lösen, werden im Prinzip die beiden oben genannten Schritte kombiniert: Man erstellt das eine Pärchen beim Öffnen der Center, aber man holt es nicht durch Einsetzen einer beliebigen ungelösten Kante auf die Oberseite, sondern man setzt genau die Kante ein, die beim Schließen der Center das zweite Pärchen bildet.

4×4: Die 8 Kanten mit der 3-2-3-Methode lösen

Dies ist der Königsweg, um die 8 verbliebenen Kantenpärchen zu bilden. Zunächst werden gleichzeitig 3 Pärchen gelöst, dann 2, und zum Schluss die noch verbliebenen 3 Pärchen. Jedenfalls ist das der prinzipielle Aufbau. Da es aber z.B. sein kann, dass anfangs schon zufällig ein gelöstes Pärchen da ist, kommt es nicht immer genau bei 3-2-3 raus. Dies zeigt Feliks Zemdegs hier auf Englisch, aber in meinem Video wird es hoffentlich auf Deutsch auch einigermaßen deutlich. Allerdings fehlt bei mir eine Erklärung der manchmal auftretenden Sonderfälle. Vielleicht mach ich das Video demnächst noch einmal neu…

5×5: Kanten lösen mit der Free-Slice-Methode

Auch für den 5×5 verwenden wir die oben schon beschriebenen Züge zum Vorwärts- und Rückwärts-Einbauen und zum Flippen der Kanten:

• Kante von oben nach rechts „vorwärts“ einbauen: F R‘ F‘ R
  
• Kante von oben nach rechts „rückwärts“ einbauen: R U‘ R‘
• Kanten-Flip rechts: R U R‘    F R‘ F‘ R

Das Schöne ist, dass diese 3 Züge die Center nicht verändern. Auch wenn die seitlichen Center gerade mal nicht zusammenstehen, sondern in horizontale Streifen zerlegt sind, bleiben diese erhalten und man kann die Center daher jederzeit wieder durch horizontale Drehungen wieder zusammenbringen.

Nur darum geht es eigentlich bei FreeSlice. Statt nach jedem (3er-)Kantenpärchen die Center zu reparieren, kann man hier etliche Pärchen nacheinander bilden, ohne sich um die Center zu scheren.

Erst wenn auf der Oberseite keine „Parkplätze“ für gelöste Kanten mehr frei sind, muss man die Center wieder herstellen und kann dann zwei weitere ungelöste Kanten nach oben holen, indem man zwei gelöste in die hinteren Slots einbaut. Das Video zu diesem Abschnitt sollte dies deutlich machen.

Manchmal hat man 2 Kanten, die beide in sich geflippt sind, wie im Bild zu sehen. Dies lässt sich ganz einfach lösen, wenn beide Kanten links und rechts gegenüber stehen:

Mit einer E-Drehung die linke Mittelkante nach rechts in die andere zu lösende Kante hineindrehen. Dann diese flippen und dann mit E‘ den Vorbereitungszug zurücknehmen. Komplett also:

E (R U R‘ F   R‘ F‘ R) E‘

Ähnlich geht man vor, wenn bei den letzten beiden zu lösenden Kanten so etwas übrig bleibt wie rechts zu sehen: Hier würde ich die rote Kante von links nach rechts über ihren passenden Mittelstein drehen (u‘ oder Uw‘) und dann den Kanten-Flip machen. Beim Zurückdrehen der u-Ebene kommen dann nicht nur die Center wieder korrekt zusammen, sondern auch die Kantensteine.

Uw‘ (R U R‘ F   R‘ F‘ R) Uw

Im Prinzip ist das ja das gleiche wie weiter oben für den 4×4 beschrieben. Auch ähnliche Fälle lassen sich so lösen, ohne dass man für jeden einzelnen Fall einen Algo lernen muss. Mal dreht man halt die obere Innenebene rüber, mal die untere, etc.
.

5×5: Parity

Sollte man am Ende nur eine solche Zickzack-Kante haben, dann ist dies OLL-Parity auf dem 5×5. Der Algorithmus dafür ist leider etwas länger, wird aber mehrfach im Video gezeigt. Die Kante muss vorne auf der Oberseite stehen, dann macht man diese Züge:

(r2 B2 U2 l) (U2 r‘ U2 r) (U2 F2 r F2) (l‘ B2 r2)

Wenn man für r2, r‘, r, l und l‘ jeweils nur die innenliegende Ebene dreht, dann tauscht dieser Algo tatsächlich NUR die beiden äußeren Kantensteine und der Rest des Würfels bleibt wie vorher. Damit kann man in einen gelösten 5×5 beispielsweise ein wunderschönes Kantenmuster hineindrehen, wenn man diesen Algo auf jeder Kante, also 12mal, anwendet (was auch eine gute Übung ist).

Schneller und einfacher geht es zum Lösen des Cubes allerdings, wenn man bei den genannten Rechts- und Linksdrehungen stattdessen Rw2, Rw‘, Rw, Lw und Lw‘ dreht, also jeweils die angrenzende Außen-Ebene mitdreht. Dann tauscht er zwar zusätzlich noch zwei komplette Kanten und zwei Ecken, aber beim noch nicht fertig gelösten Würfel ist das ja egal. Also dreht man genaugenommen:

(Rw2 B2 U2 Lw) (U2 Rw‘ U2 Rw) (U2 F2 Rw F2) (Lw‘ B2 Rw2)

Hier nun mein ziemlich mittelmäßiges Video über das Lösen der letzten 8 Kanten auf dem 4×4 (bis Minute 15) und auf dem 5×5:

Da es auf dem 5×5 kein PLL-Parity gibt, ist der 5×5 am Ende dieses Schrittes schon so weit, dass man ihn wie einen 3×3 lösen kann, wenn man ab hier nur noch die Außen-Ebenen bewegt. Daher werden die beiden 5×5 im Video fertig gelöst. Welche Methode Ihr für den 3×3-Teil verwendet, ist eigentlich egal. Wegen des schon fertigen weißen Kreuzes ist es allerdings sinnvoll, wenn es eine Methode ist, die auch mit dem weißen Kreuz beginnt, also z.B. die Anfängermethode oder die Fridrich-Methode.

Schritt 5: Wie ein 3×3 lösen, und wenn nötig
OLL-Parity und/oder PLL-Parity beseitigen

Auch der 4×4 wird nun wie ein 3×3 gelöst. Bei ihm ist allerdings erst mit Erreichen der dritten Ebene erkennbar, ob es zu Parities kommt.

4×4: OLL-Parity

Zur Erinnerung: Wenn auf dem 3×3 die unteren beiden Ebenen gelöst sind, zeigen entweder 0 oder 2 oder 4 gelbe Kanten nach oben. Sollten es 1 oder 3 gelbe Kanten sein, dann ist der Würfel falsch zusammengebaut und somit unlösbar.

Auf dem 4×4 kommt es allerdings in 50% der Fälle vor, dass es 1 oder 3 gelbe Kantenpaare gibt, die nach oben zeigen. Dann haben wir OLL-Parity und müssen dies erst beseitigen, bevor wir den 4×4 wie einen 3×3 lösen können.

Freundlicherweise geht dies mit dem gleichen Algorithmus wie beim 5×5. Das Kantenpaar, das gewendet werden soll, steht wieder vorne auf der Oberseite und dann der bekannte Algorithmus:

(r2 B2 U2 l) (U2 r‘ U2 r) (U2 F2 r F2) (l‘ B2 r2)

Wie beim 5×5 gilt auch hier: In dieser Form wendet er NUR das gelbe Kantenpaar. Wenn man aber die äußeren Ebenen mitdreht (Rw2, Lw, etc.), dann dreht es sich einfacher, aber einige andere (noch nicht gelöste) Ecken und Kantenpaare bewegen sich auch.

Eleganter zu drehen auf dem 4×4 ist allerdings folgender Algo:

(Rw U2 x) (Rw U2 Rw U2) (Rw‘ U2 Lw U2) (Rw‘ U2 Rw U2) (Rw‘ U2 Rw‘)

Ich finde, der lernt und dreht sich besser als der Parity-Zug vom 5×5 mit seinen B-Drehungen.

4×4: PLL-Parity

Ebenfalls in 50% der Fälle kommt es vor, dass beim Positionieren der Kantenpaare bzw. Ecken auf der Oberseite eine Situation übrig bleibt, die auf dem 3×3 unmöglich wäre. Dies können sein:

• 2 gegenüber stehende Kanten vertauscht, oder
• 2 nebeneinander stehende Kanten vertauscht, oder
• 2 Ecken vertauscht

Mit dem folgenden Algorithmus löst man den ersten Fall. Die beiden Kanten müssen auf der Oberseite vorne und hinten stehen, dann werden sie getauscht:

r2 U2   r2 Uw2   r2 u2

Wichtig: r2 bezeichnet hier immer NUR die Drehung der inneren Ebene, also ohne die Außenebene. Nach dem ersten r2 wird die oberste Ebene um 180° gedreht, nach dem zweiten r2 die beiden oberen Ebenen und nach dem dritten r2 nur die zweitoberste Ebene (was man ganz gut ausführen kann, wenn man Uw2 + U2 dreht).

Mit dem gleichen Algo löst man auch die anderen Fälle. War die obere Ebene zuvor mit 3×3-Zügen unlösbar, ist sie jetzt lösbar. Und umgekehrt. 🙂

Im Prinzip reicht dies zum Lösen. Aber man kann dies noch ein wenig abkürzen:

Hat man den Fall, dass die beiden zu tauschenden Kanten nebeneinander stehen, kann man es auch gleich komplett erledigen, indem man den Sexy Move als Vorbereitungszug macht, dann den PLL-Parity-Zug und dann den Sexy Move wieder rückwärts:

R U R‘ U‘ + (r2 U2 r2 Uw2 r2 u2) + U R U‘ R‘

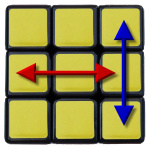Im dritten Fall, bei dem ausschließlich 2 Ecken vertauscht sind, kann man den Parity-Zug quasi zwischen den beiden vertauschten Ecken anwenden und dann hat man die Ausgangssituation für einen T-Perm:

(R U R‘ U‘) (R‘ F R2) (U‘ R‘ U‘) (R U R‘ F‘)

Komplett also: Vertauschte Ecken nach vorne auf der Oberseite halten und dann:

(r2 U2 r2 Uw2 r2 u2) + y‘ + (R U R‘ U‘) (R‘ F R2) (U‘ R‘ U‘) (R U R‘ F‘)

Natürlich geht es auch umgekehrt: Erst aus den getauschten Ecken mit dem T-Perm getauschte Kantenpaare machen und diese dann mit dem PLL-Parity-Algo lösen.

Im Video wird dies hoffentlich deutlich:

So, das war’s für den 4×4 und den 5×5. Nicht perfekt, ich weiß. Aber gerne könnt Ihr mir die noch unklaren Punkte in die Kommentare schreiben. Nicht nur, dass ich dort Fragen gerne beantworte. Auch wäre es eine Hilfe, wenn ich insbesondere die beiden letzten Videos vielleicht verbessert neu aufnehmen sollte.

Jedenfalls wünsche ich Euch viel Spaß mit dem 4×4 und dem 5×5.

PS: Im folgenden Artikel gibt es 2 Videos, die jeweils mehrere Beispiel-Solves für den 4×4 und für den 5×5 zeigen.