Wie viele Drehungen braucht eine Zauberwürfel-Lösung mindestens?

Im dritten Teil der Serie über Zahlen, Daten und Fakten zum Zauberwürfel geht es diesmal um optimale Lösungen, also mit möglichst wenig Drehungen.

Außer dem „normalen“ Speedcubing, also dem Lösen des Zauberwürfels in wenigen Sekunden, gibt es auf offiziellen Wettbewerben auch die Disziplin FMC, was für „Fewest Move Count“ steht. Es geht also darum, einen (nach einer „Misch-Anleitung“, dem sogenannten „Scramble“) verdrehten Zauberwürfel mit möglichst wenigen Drehungen zu lösen. Dafür haben die Teilnehmer eine ganze Stunde Zeit, um mit Papier und Stift und mehreren Cubes, sowie ziemlich viel Theorie und Techniken im Kopf, eine möglichst kurze Lösung zu finden. Die 100 besten Teilnehmer weltweit schaffen durchschnittlich Lösungen zwischen 21 und 28 Zügen. Ein gutes Dutzend FMC-Teilnehmer hat auch schon in Einzelfällen Lösungen unter 20 Zügen gefunden.

Weltmeister in „FMC Single“ ist übrigens seit 2019 Sebastiano Tronto, den ich schon bei mehreren Competitions getroffen habe, und der eine Lösung mit 16 Zügen gefunden hat. Reto Bubendorf, den ich auch schon mehrfach getroffen habe, steht mit einem „FMC Average“ (Durchschnitt aus 3 Versuchen) von 23 Drehungen derzeit auf Platz 7 der Weltrangliste. Wer sich näher dafür interessiert, wie FMC geht: In Folge 25 des Freshcuber-Podcasts hat er es ausführlich erklärt.

Wenn es also Menschen gibt, die den Zauberwürfel in 16 oder 23 Zügen lösen können, stellt sich natürlich die Frage: Gibt es eine Grenze für die notwendige Anzahl von Zügen, die ein „richtig ordentlich verdrehter“ Zauberwürfel zum Lösen benötigt? Kann man durch stundenlanges Mischen den Cube überhaupt „besonders kompliziert“ verdrehen? Hatten Sebastiano, Reto und die vielen anderen, die es in unter 30 Zügen geschafft haben, einfach nur Glück mit einfachen Scrambles?

Oder anders gefragt: Wie viele Drehungen würde Gott bei FMC brauchen, angenommen er wäre wirklich allwissend, findet daher für jeden Scramble die optimale Lösung? Vielleicht hat er ja sogar irgendwo im Universum die 260 Lichtjahre lange Reihe von 43 Trillionen Cubes versteckt. 😉 Also egal welcher Scramble: Wie lautet diese „Gotteszahl“ für den 3×3-Zauberwürfel, also die maximale Länge optimal kurzer Solves?

Zunächst muss man sich aber einigen, was man als „Drehung“ definiert. Zählt eine 180-Grad-Drehung (Doppeldrehung, z.B. U2) einer Cube-Seite als eine Drehung oder als zwei mal 90 Grad, also zwei Drehungen (U + U)? Die übliche Variante ist, dass eine 180°-Doppeldrehung als einzelne Drehung zählt. So wird auch bei den FMC-Wettbewerben gerechnet.

Diese Gotteszahl hat Mathematiker schon früh interessiert. Von 1981 bis 2008 fiel die Annäherung an die Gotteszahl von zunächst 52 auf 22. Auf der Seite www.cube20.org ist eine Übersicht der Daten zu finden. Das Problem ist ja, dass ein einzelner Solve mit 16 oder 23 Zügen nicht beweist, dass es nicht auch kompliziertere Solves gibt. Die Antwort wissen wir jedenfalls seit gut 10 Jahren: Im Juli 2010 berechneten die drei US-Amerikaner Tomas Rokicki, Morley Davidson und John Dethridge und der Darmstädter Herbert Kociemba (mit 35 CPU-Jahren Computerzeit, die Google zur Verfügung gestellt hatte), dass jede Stellung in höchstens 20 Zügen gelöst werden kann. Das ist also die Gotteszahl. Egal, wie sehr ein Zauberwürfel verdreht ist, Gott (oder Sebastiano) könnten ihn mit maximal 20 Drehungen lösen.

Herr Kociemba ist in der Cubing-Szene auch durch sein Programm Cube Explorer berühmt, das mit den Ergebnissen, die es liefert, schon meist sehr nahe an die Gotteszahl 20 herankommt. Oder diese sogar unterbietet – doch dazu gleich mehr. Er hat mir auch geholfen bei einer anderen mathematischen Fragestellung, betreffend das 15-Puzzle (auch  Schiebepuzzle oder Klotski Puzzle genannt). Ergebnis ist das „Frisch-Kociemba-Gesetz magischer Schiebequadrate“ (siehe ebenfalls Freshcuber-Podcast, Folge 25).

Wenn nun die Gotteszahl 20 beträgt, wie kann es dann sein, dass z.B. Sebastiano Tronto eine Lösung mit 16 Zügen gefunden hat?

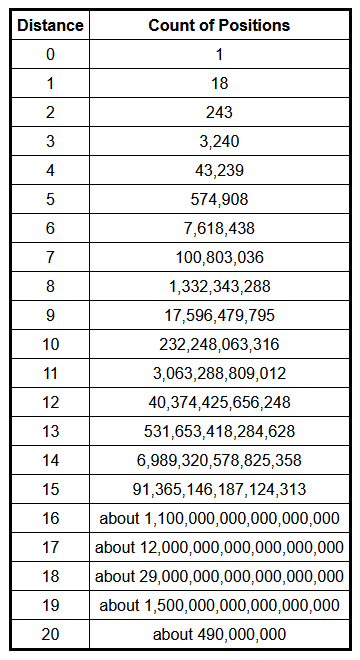
Nun, offenbar war es einer der Scrambles, die eben nicht die maximale Zahl von 20 Drehungen für die Lösung brauchten. Auf www.cube20.org findet sich die rechts abgebildete Tabelle, die einen wunderschönen „Tannenbaum“ zeigt. Von den 43 Trillionen Stellungen insgesamt können etwa 41 Trillionen Stellungen mit 17 oder 18 Zügen gelöst werden. „Nur“ 1,5 Trillionen Stellungen benötigen 19 Züge. Und 490 Millionen Stellungen erfordern tatsächlich mindestens 20 Züge. Das ist nur eine von 88 Milliarden Positionen. Deshalb sind Scrambles, bei denen FMC-Ergebnisse von 18 oder weniger möglich sind, bei Weitem in der Mehrheit.

Um Sebastianos 16 zu unterbieten, braucht man außer viel Können auch eine dicke Portion Glück. Nur knapp 99 Billiarden der 43 Trillionen Scrambles sind mit weniger als 16 Zügen lösbar. Einen solchen Scramble erhält man also nur durchschnittlich bei jedem 437sten Versuch. Das hier waren übrigens Sebastianos Scramble und seine gefundene Lösung:

• Scramble: R‘ U‘ F D2 L2 F R2 U2 R2 B D2 L B2 D‘ B2 L‘ R‘ B D2 B U2 L U2 R‘ U‘ F
• Lösung: D2 F‘ D2 U2 F‘ L2 D R2 D B2 F L2 R‘ F‘ D U‘

Wer die Zauberwürfel-Notation kennt, kann es gerne ausprobieren. Sebastiano Tronto hat hier mit 16 Zügen den mit 26 Drehungen vermischten Zauberwürfel gelöst. Laut seiner Aussage im Video ist die 16 für diesen Scramble die kürzestmögliche, also optimale, Lösung. Gott™ hätte es auch nicht kürzer hinbekommen – nur schneller.

Womit wir bei der Frage sind, ob die kürzeste Lösung auch notwendigerweise die schnellste Lösung ist? Die Antwort lautet Nein. Zum Einen ist es halt nicht möglich, in 15 Sekunden Vorbereitungszeit eine optimale Lösung wie bei FMC zu finden. Und zum Anderen kann es sehr wohl sein, dass die schnellen Speedcuber zum Beispiel für Sebastianos obigen Scramble eine Lösung finden würden, die zwar ein paar Züge mehr hat, sich dafür aber besser drehen lässt.

Der bisher schnellste 3×3 Single Weltrekord stammt von 2018, als Yusheng Du einen Würfel in 3,47 Sekunden löste. 27 Züge machte er in dieser Zeit (mit einem sehr glücklichen Scramble), wie die Analyse im Video zeigt. Für die 4,22 Sekunden, die Speedcubing-Legende Feliks Zemdegs einige Monate vorher geschafft hatte, brauchte er 38 Züge (Video). Das sind 9 Drehungen pro Sekunde.

Für einen Speedsolve sind 38 Drehungen extrem effizient; meine eigenen Solves haben meist eher die doppelte Zugzahl (weil ich nicht so viele Abkürzungen kenne wie Feliks). Und weil ich selbst eher bei 2-3 Drehungen pro Sekunde bin, brauche ich halt eher so 25 statt 5 Sekunden. Ein durchschnittlicher Speedsolve mit der üblichsten Methode (CFOP) hat meist so etwa 60 Züge. Dass es theoretisch auch mit 18-20 Zügen gehen würde, nützt einem da gar nichts. 🙂

Auf die Weltrekorde, nicht nur von Yusheng Du und Feliks Zemdegs, lohnt sich noch ein etwas genauerer Blick. Um Rekorde geht es also im nächsten Artikel der Serie über Wissenwertes rund um Zauberwürfel und Speedcubing.

Zum Abschluss dieses Themas hier noch ein Blick auf einen besonders interessanten Fall, den sogenannten Superflip, ein bekanntes Zauberwürfel-Muster. Auf BigCubes wie dem hier gezeigten 11x11x11 sieht er aus, wie eine karierte Tischdecke. Aber wir schauen jetzt lieber auf den kleineren Cube, den normalen 3x3x3.

Wie man erkennen kann, stehen alle Ecksteine korrekt am richtigen Platz, aber alle Kantensteine sind an ihrem Platz verdreht. Und obwohl 8 der 20 Steine bereits gelöst sind und nur noch die 12 Kanten falsch stehen, benötigt der Superflip mindestens 20 Züge für die Lösung. Dies wurde bereits 1995 bewiesen; es war die neue Untergrenze für die gesuchte Gotteszahl. Und damit war die später bestätigte 20 ein heißer Kandidat für diesen Titel.

Es hat aber noch 15 Jahre gedauert um zu belegen, dass es keine einzige Stellung auf dem Cube gibt, die 21 oder mehr Züge benötigt. Hätte ja gut sein können, dass sich in der 260 Lichtjahre langen Reihe doch noch ein komplizierterer Fall versteckt.

Wer den Superflip ausprobieren möchte, hier ist der Algorithmus mit 20 Drehungen:

R L U2 F   U‘ D F2 R2   B2 L U2 F‘   B‘ U R2 D   F2 U R2 U

In meiner Sammlung von 24 Zauberwürfel-Mustern zeige ich den Superflip allerdings mit einer Drehvariante, die wesentlich einfacher auswendig zu lernen ist, obwohl sie länger ist als die obige Variante. Dafür kann man sie mit einem hübschen Fingertrick zeigen.

Wer noch etwas mehr über die Gotteszahl 20 erfahren möchte (beispielsweise über die Spitze der oben gezeigten „Tannenbaum“-Tabelle, kann ja gerne mal in die Folge 26 des Freshcuber-Podcasts hineinhören. Ab Minute 11:40 geht es da um dieses Thema, aber schon vorher in dieser Folge gibt es einen neuen FMC-Weltrekord zu vermelden.

Zusammenfassung:

• Egal, wie lange ein Zauberwürfel verdreht wurde: Kein Würfel ist jemals mehr als 20 Züge vom gelösten Zustand entfernt. Leider sieht man bei den ersten Drehungen aber nicht, ob sie näher zur Lösung führen oder nicht.
• Diese Zahl 20, also die maximale Länge, die ein verdrehter Zauberwürfel vom gelösten Zustand entfernt ist, nennt man Gotteszahl (für den normalen 3x3x3-Zauberwürfel), denn wenn man entsprechend allwissend wäre, könnte man jeden 3×3-Würfel mit der kürzestmöglichen Anzahl Drehungen lösen.
• Seit 1995 ist bekannt, dass die Gotteszahl mindestens 20 betragen muss. Seit 2010 ist mathematisch bestätigt, dass sie genau 20 beträgt.
• Die meisten verdrehten Stellungen benötigen aber gar nicht 20, sondern nur 18 oder 17 Drehungen für die optimal kurze Lösung.
• Mit hohem Aufwand an Zeit und Techniken finden die besten Teilnehmer beim Fewest Moves Wettbewerb (FMC) Lösungen, die schon recht nahe an die optimale Zugzahl für den jeweiligen Scramble herankommt.
• Für das Speedcubing spielt die Gotteszahl 20 allerdings keine Rolle, da man in wenigen Sekunden nicht die optimale Lösung finden kann. Speedcubing-Lösungen haben oft so etwa 60 Drehungen. Bei entsprechender Drehgeschwindigkeit der schnellsten Speedcuber sind dennoch Zeiten unter 7 Sekunden möglich.